Linear-Time Sorter for FPGAs
Sorting algorithms are an old hat in the comp-sci community. Running times on the fastest of these algorithms is usually O(Nlog(N)) on a single core. I thought, with an FPGA, why not try a parallel approach in hardare to bring the running time down to O(N)?
A few head-scratching evenings later–behold–the Linear-Time-Sorter was born! I’m jazzed to mock this up as an SPI-peripheral for a microcontroller. Feel free to make use of the source files as you need.
Behavior
Sorting is performed in linear time as the unsorted array is being serially clocked into the sorter. With this scheme, the sorting is done as soon as the unsorted array has finished being input into the sorting logic. In that sense, it can be read out immediately after it’s been clocked in! The running time on this algorithm is O(N), where N is the number of clock cycles needed before the unsorted array has been sorted.
Parameters
- DATA_WIDTH is width of the input word value in bits. While DATA_WIDTH can be anywhere from 1 to N bits, the spi wrapper in my source files limits bit values to a multiple of bytes (8, 16, 32) such that each word can be transferred as a series of 1 or more bytes within an spi frame.
- SIZE is the maximum number of words that can be sorted by the sorter. An unsorted input array may be any length of words up to SIZE words long.
Altera Quartus’ RTL viewer lets us visualize the generated logic once we’ve tweaked the parameters above. Here’s a sample of a 10-sorter where SIZE = 10.
(A fair forewarning that wires don’t get visualized very cleanly by the autogenerated graphic)
The Interface
For convenience, I’ve wrapped up the sorter logic inside an SPI interface. N unsorted array elements are accepted serially via N sequential spi transfers while the WRITE pin is asserted. The sorted array can then be immediately clocked out via N more spi transfers while the WRITE pin is released.
For more details on the nuts and bolts behind how the SPI Interface works, check out my step-by-step guide (PDF) that I wrote earler.
The Algorithm
Questions asked in Parallel
The algorithm boils down to two questions asked in parallel across all cells. For each cell, we must answer the questions:
- am I empty or occupied?
- If occupied, is my current value pushed by either the previous cell value or the new value to be sorted?
Simultaneously, each cell also needs the answer to both of these questions from the previous cell.
Hence, we can build a logical block designed for this specific purpose that answers these questions within a single clock cycle:
Sorting Cell IOs
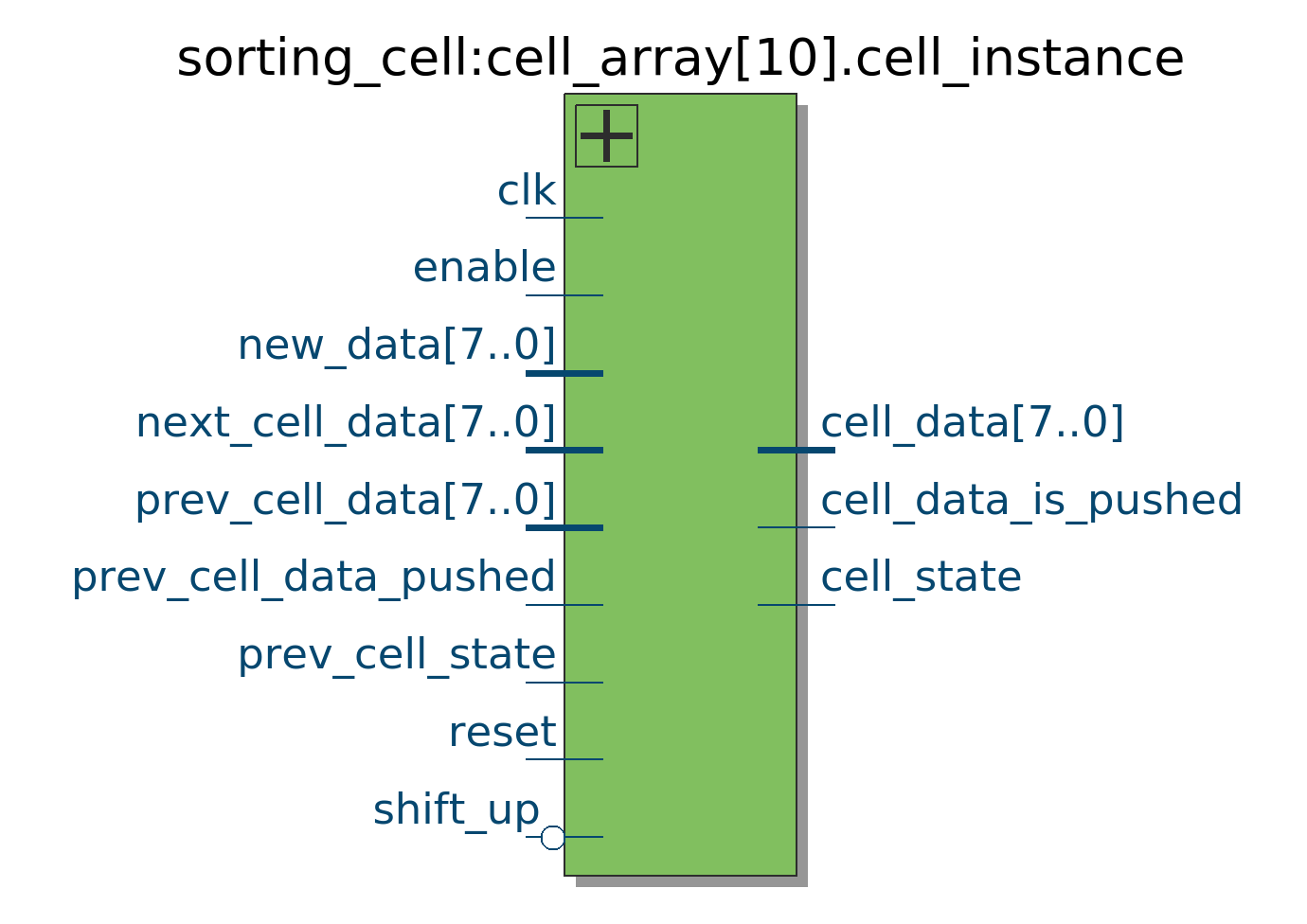
(Ignore the shift_up and next_cell_data inputs as they are only used for clocking the data out after it’s been sorted.)
Answering the first question involves us keeping track of the cell state as either empty or occupied. Upon reset, the cell state is empty, but if data enters the cell it is occupied from that point onward. Implementation is a simple two-state state machine.
Answering the second question: “am I pushed” is as easy as asking whether or not the new value is strictly less-than the current cell value and the current cell is already occupied:
assign new_data_fits = (new_data < cell_data) || (cell_state == EMPTY);
assign cell_data_is_pushed = new_data_fits & (cell_state == OCCUPIED);
Finally we’ll need to make agreements on what happens based on these inputs.
- If the previous cell value is pushed, the input cell must take the previous cell’s value.
- If the previous cell is full and the current cell is empty and previous cell data is pushed, then the cell must take the previous cell’s data.
- If the previous cell is full, the current cell is empty, and the previous cell data was not pushed, then the current cell must take the input data since it is assumed that it is the first empty cell at the bottom of the cell array and the input value is the largest value seen so far since it didn’t fit in any of the previous cells.
- In all other cases, the cell keeps its original data.
This logic ends up manifesting itself as a priority decoder:
logic [4:0] priority_vector;
assign priority_vector [4:0] = {shift_up, new_data_fits, prev_cell_data_pushed,
cell_state, prev_cell_state};
/// ... Source File truncated for brevity ...
casez (priority_vector)
'b0?1??: cell_data <= prev_cell_data;
'b0101?: cell_data <= new_data;
'b0?001: cell_data <= new_data;
'b1????: cell_data <= next_cell_data;
default: cell_data <= cell_data;
endcase
Example: a “4-sorter” sorting a 4-element array
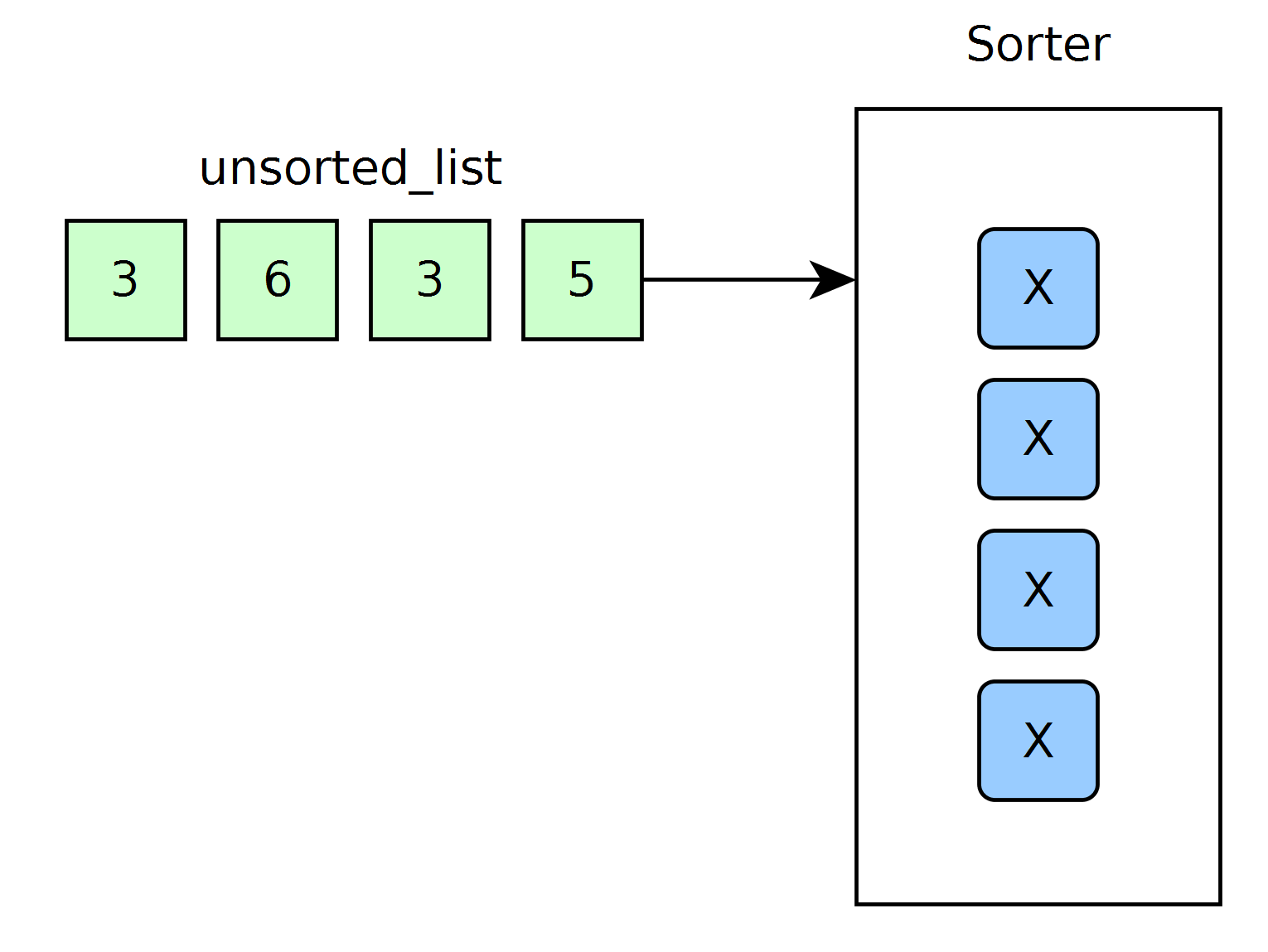
By setting the SystemVerilog parameters DATA_WIDTH to be 8 and SIZE to be 4, I can generate a “4-sorter” that can sort arrays up to length 4 in linear time. Here’s a block-diagram of the test setup:
The FPGA logic is wrapped up inside the sorter block, and cells are marked with an x to indicate empty. I’ve tossed out the SPI interface for now just to highlight the inputs and outputs of the cells to show how they interact with each other.
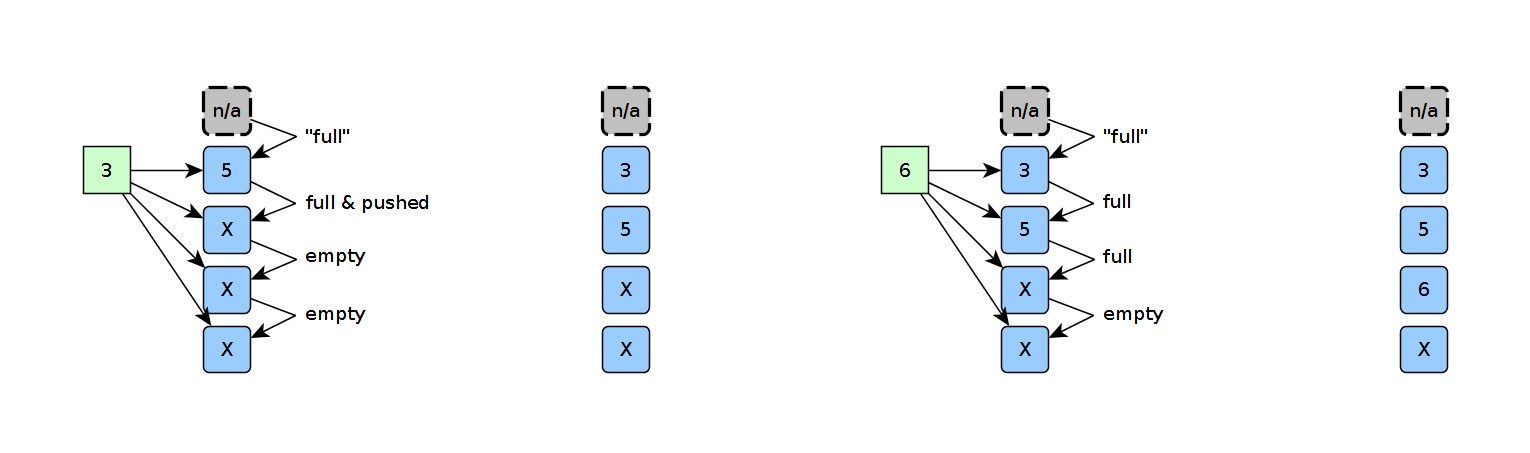
Let’s start by following the sorting behavior as we input unsorted elements in serially. When we try to insert the first element, each cell compares it to the current stored element in that cell and answer the questions:
- Am I empty or occupied?
- Is my data pushed by the previous cell’s value or the new value to be sorted?
Meanwhile it receives the answers to these questions from the previous cell:
- Is the previous cell occupied?
- Is the previous cell pushing its cell value?
The answers to these questions happen within a single clock cycle. (Senders and receivers of this information, as well as what information was sent, are depicted with arrows below.)
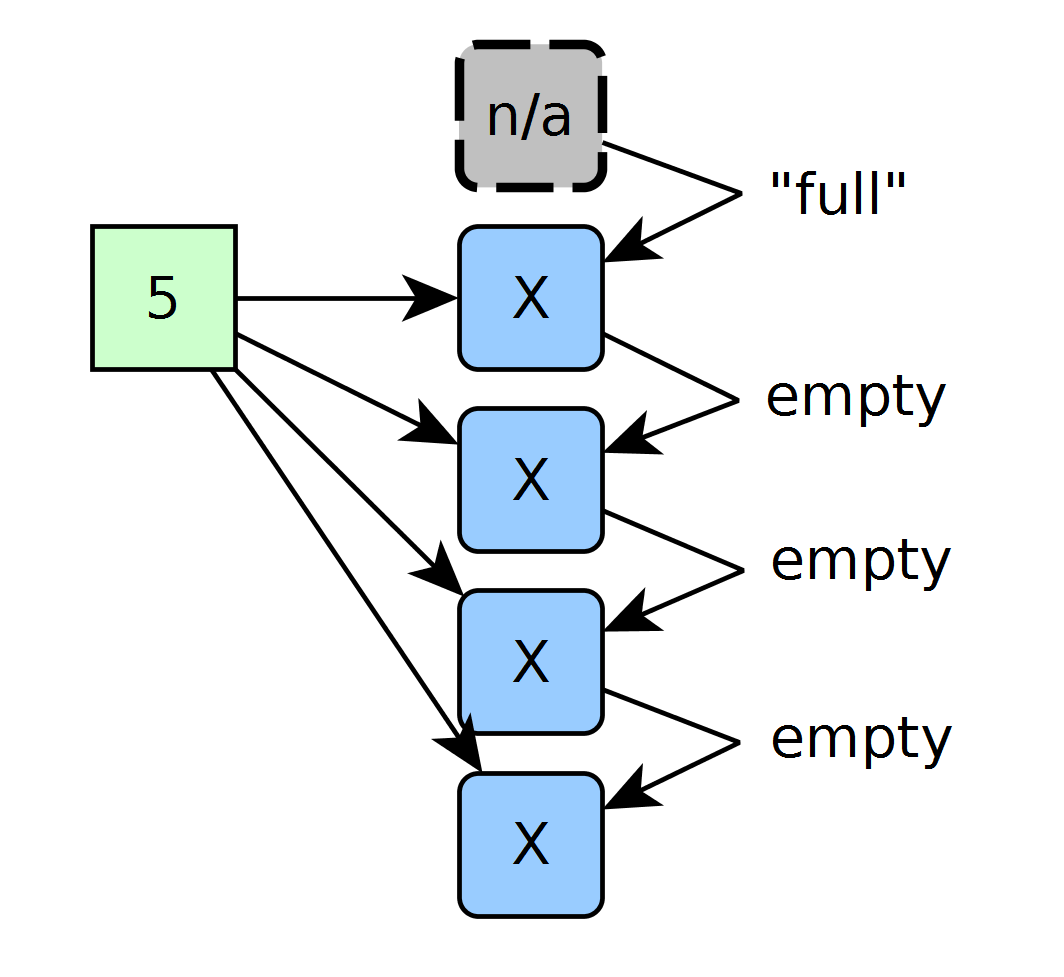
Upon reset, all elements start off as empty. To force the first cell to take the first element, I’ve tied that element’s prev_cell_data_pushed input HIGH. In that sense, with an empty array input, the first inserted element will always be claimed by the first empty cell. While other cells are empty, they do not take the first element because each of their respective previous cells are also empty.
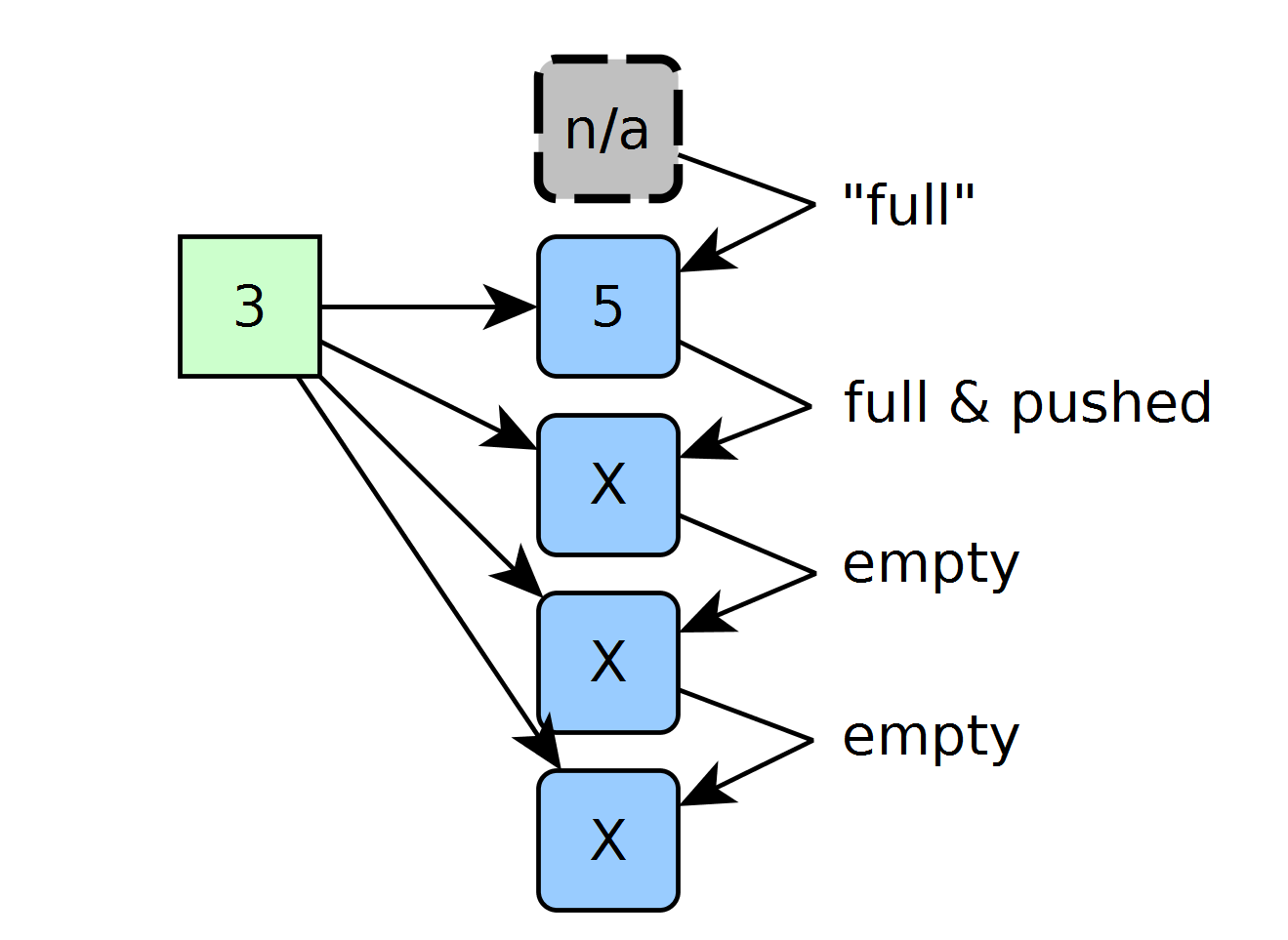
On the next clock cycle, we’re ready to insert another element and sort it. Again, each cell asks the same questions and receives the answers to those questions from the previous cell. Since 3 is less-than 5, the cell holding 5 kicks its data down to the next cell and takes the 3 instead.
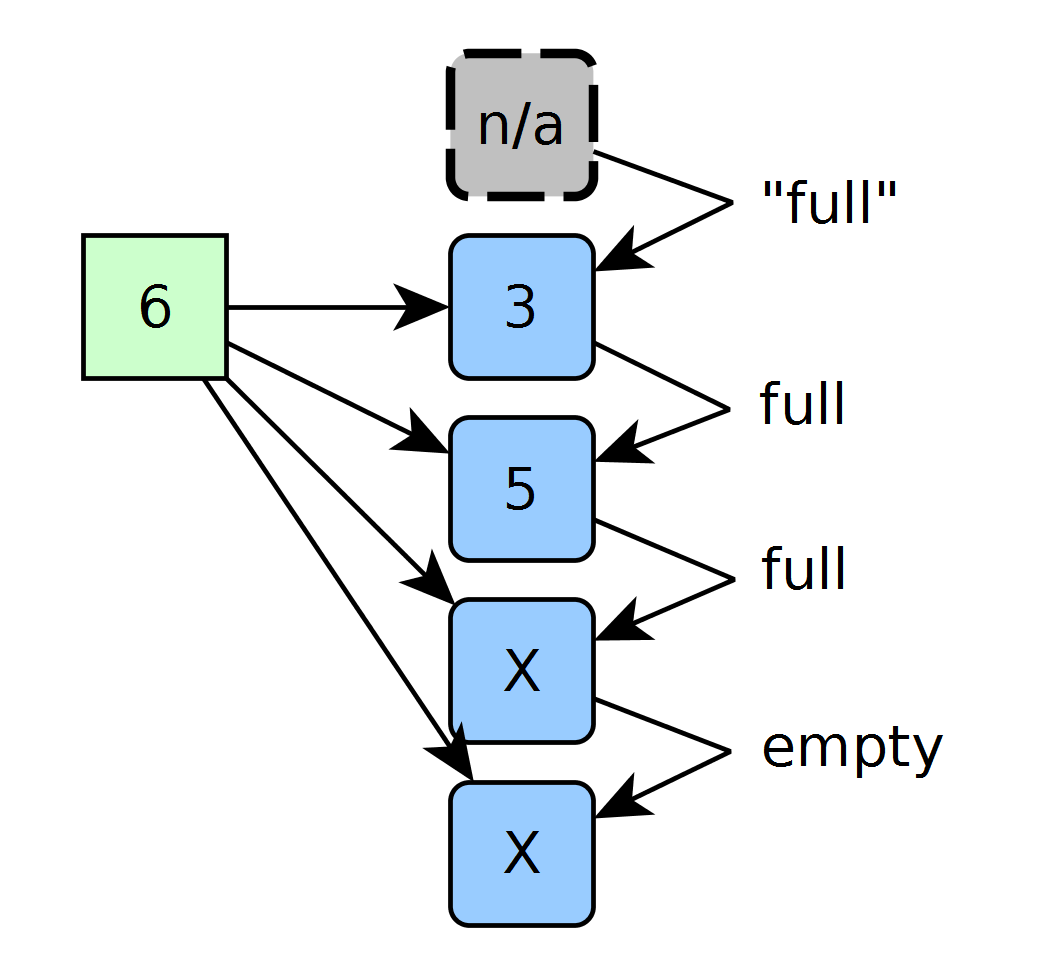
On the next clock cycle we insert a 6. Since all occupied cells contain values less than 6, the 6 goes into the first empty slot.
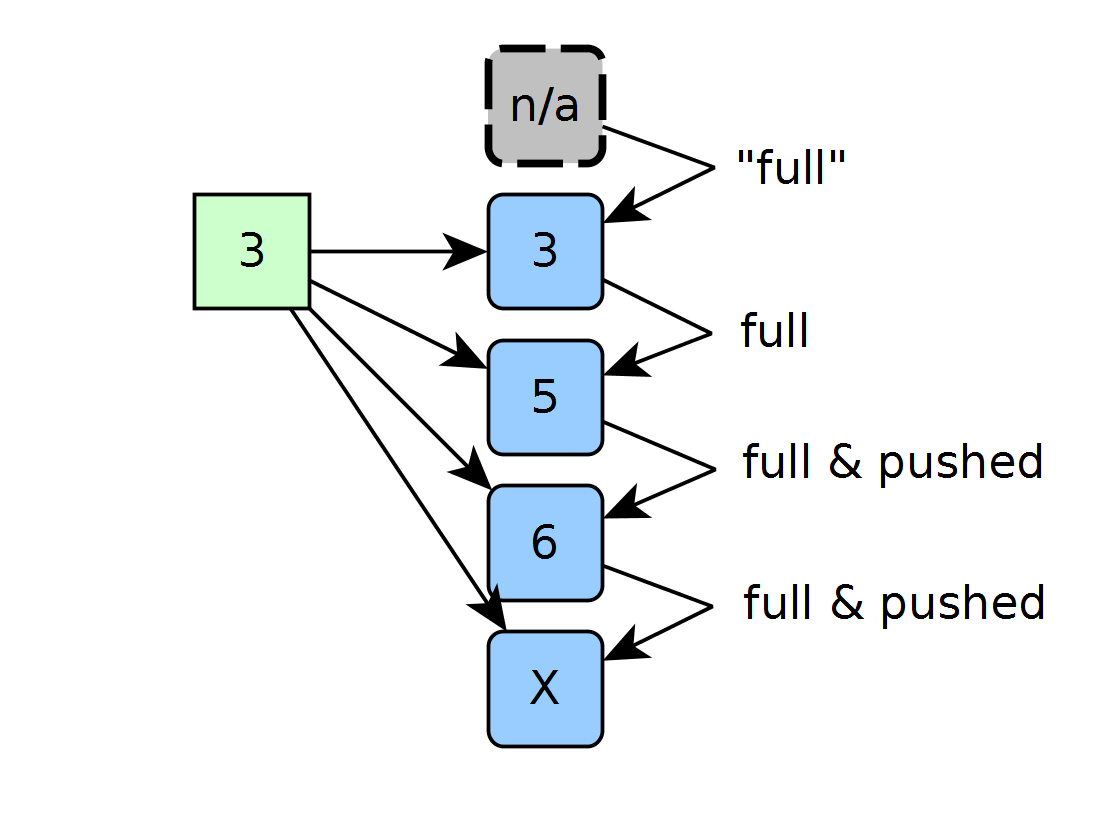
On the next clock cycle, we get yet another value, but this time that value forces a “push” on values 5 and 6 since 3 fits in both 5 and 6’s spots. Here, the new 3 claims the spot currently holding a 5. While both the cell with 5 and the cell with 6 could both accomodate the new 3, the 3 fits into the former of the two because the cell holding 6 must take the previous pushed value over all other cases.
The Takeaway
It works! If you’ve got a Teensy and an FPGA floating around your bench, feel free to give it a shot from the source files and let me know what you think.
Walking in, I tried to nail down the base case of the inputs-and-outputs of a single cell. Once I could prove that the IOs worked for one, I could prove that they’d work for N and so on! In the current source code state, I can scale the maximum capacity of the sorter with a single parameter, growing the complexity of the system larger than anything I’d be able to keep track of in my head all at once! Here lies the beauty of modular design. If we can solidify the agreements between each of the most fundamental components of our system, we can guarantee and predict their behavior when those same components work together in a largers system.
Even though the problem of fast-sorting seems complicated, the building blocks that form the solution don’t have to be.
On the other hand, while this solution saves time with a parallel approach, we’re paying a different price in consumed FPGA resources. Weighing time and space is a game I’ll likely need to play in the future.